Contoh soal latihan bangun datar kelas 4

Menjelajahi Dunia Bangun Datar: Contoh Soal Latihan untuk Kelas 4 SD

Matematika seringkali dianggap sebagai pelajaran yang rumit, namun sebenarnya ia adalah gerbang menuju pemahaman dunia di sekitar kita. Salah satu topik yang sangat mendasar dan sering kita jumpai dalam kehidupan sehari-hari adalah bangun datar. Dari jendela rumah, ubin lantai, hingga roda sepeda, semua adalah contoh konkret dari bangun datar.

Bagi siswa kelas 4 SD, memahami bangun datar bukan hanya tentang menghafal rumus, tetapi juga tentang mengenali bentuk, memahami sifat-sifatnya, dan mampu menghitung keliling serta luasnya. Artikel ini dirancang khusus untuk membantu siswa kelas 4, orang tua, dan guru dalam memahami konsep bangun datar melalui serangkaian contoh soal latihan yang komprehensif. Mari kita mulai petualangan kita di dunia bangun datar yang seru ini!

Mengulang Konsep Dasar Bangun Datar

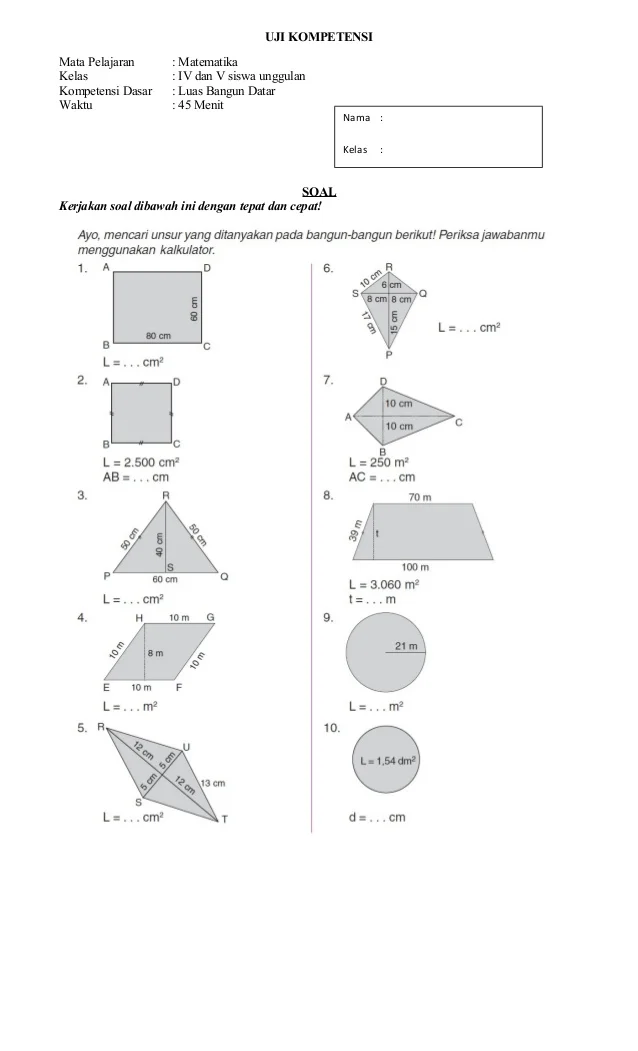
Sebelum melangkah ke soal latihan, mari kita segarkan kembali ingatan kita tentang apa itu bangun datar dan elemen-elemen pentingnya.

Apa Itu Bangun Datar?
Bangun datar adalah bangun dua dimensi yang hanya memiliki panjang dan lebar, tanpa ketebalan. Bentuk-bentuk ini bisa kita gambar di atas kertas.

Elemen-elemen Penting Bangun Datar:
Setiap bangun datar memiliki elemen-elemen dasar yang membentuknya:

1. Sisi: Garis yang membentuk tepi bangun datar.
2. Sudut: Titik pertemuan dua sisi.
3. Titik Sudut: Titik di mana dua sisi bertemu dan membentuk sudut.

Jenis-jenis Bangun Datar yang Umum Dikenal di Kelas 4:

• Persegi:

  • Memiliki 4 sisi yang sama panjang.
  • Memiliki 4 sudut siku-siku (90 derajat).
  • Contoh: Ubin lantai, papan catur.

• Persegi Panjang:

  • Memiliki 4 sisi, di mana sisi yang berhadapan sama panjang.
  • Memiliki 4 sudut siku-siku (90 derajat).
  • Contoh: Pintu, buku, lapangan bulu tangkis.

• Segitiga:

  • Memiliki 3 sisi.
  • Memiliki 3 sudut.
  • Ada berbagai jenis segitiga (sama sisi, sama kaki, siku-siku, sembarang), namun di kelas 4 fokus pada konsep dasarnya.
  • Contoh: Potongan pizza, rambu lalu lintas.

• Lingkaran:

  • Memiliki 1 sisi lengkung yang tak berujung.
  • Tidak memiliki sudut maupun titik sudut.
  • Memiliki titik pusat, jari-jari (r), dan diameter (d). Diameter adalah dua kali jari-jari (d = 2r).
  • Contoh: Roda, koin, jam dinding.

• Bangun Datar Lain (Pengenalan):

  • Jajar Genjang: Sisi-sisi yang berhadapan sejajar dan sama panjang, sudut yang berhadapan sama besar.
  • Trapesium: Memiliki sepasang sisi sejajar.
  • Belah Ketupat: Semua sisinya sama panjang, sudut yang berhadapan sama besar.

Keliling dan Luas Bangun Datar

Dua konsep penting dalam bangun datar adalah keliling dan luas.

• Keliling:

  • Keliling adalah total panjang semua sisi yang mengelilingi sebuah bangun datar. Bayangkan Anda berjalan mengelilingi sebuah lapangan, jarak yang Anda tempuh adalah keliling lapangan tersebut.
  • Rumus Keliling:
    • Persegi: Keliling = 4 x sisi
    • Persegi Panjang: Keliling = 2 x (panjang + lebar)
    • Segitiga: Keliling = sisi1 + sisi2 + sisi3
    • Lingkaran (Keliling Lingkaran/Keliling): Keliling = 2 x π x jari-jari (r) atau π x diameter (d). (Nilai π (pi) seringkali dibulatkan menjadi 22/7 atau 3.14).

• Luas:

  • Luas adalah ukuran seberapa banyak permukaan yang ditutupi oleh sebuah bangun datar. Bayangkan Anda mengecat dinding, area yang Anda cat adalah luas dinding tersebut.
  • Rumus Luas:
    • Persegi: Luas = sisi x sisi
    • Persegi Panjang: Luas = panjang x lebar
    • Segitiga: Luas = ½ x alas x tinggi

Pentingnya Satuan Ukuran:
Saat menghitung keliling atau luas, jangan lupakan satuan ukurannya!

• Untuk keliling, satuannya adalah satuan panjang (misalnya cm, m, km).
• Untuk luas, satuannya adalah satuan luas (misalnya cm², m², km²).

Contoh Soal Latihan Bangun Datar untuk Kelas 4 SD

Sekarang, mari kita terapkan pemahaman kita melalui serangkaian soal latihan. Setiap soal akan disertai dengan pembahasan lengkap untuk membantu Anda memahami langkah-langkah penyelesaiannya.

Bagian 1: Identifikasi dan Properti Bangun Datar

Soal 1:
Perhatikan gambar bangun datar di bawah ini (bayangkan ada gambar):
A. Segiempat dengan semua sisi sama panjang dan sudut siku-siku.
B. Bangun dengan 3 sisi.
C. Bangun dengan satu sisi lengkung.
D. Segiempat dengan sisi berhadapan sama panjang dan sudut siku-siku.

Tentukan nama bangun datar dari deskripsi di atas!
a. A = ………………..
b. B = ………………..
c. C = ………………..
d. D = ………………..

Pembahasan Soal 1:
Untuk menjawab soal ini, kita perlu mengingat ciri-ciri atau properti dasar setiap bangun datar.
a. A adalah Persegi, karena memiliki semua sisi sama panjang dan sudut siku-siku.
b. B adalah Segitiga, karena memiliki 3 sisi.
c. C adalah Lingkaran, karena memiliki satu sisi lengkung.
d. D adalah Persegi Panjang, karena memiliki sisi berhadapan sama panjang dan sudut siku-siku.

Soal 2:
Sebuah bangun datar memiliki ciri-ciri sebagai berikut:

• Memiliki 4 titik sudut.
• Keempat sudutnya adalah sudut siku-siku.
• Memiliki 2 pasang sisi yang sama panjang.

Nama bangun datar tersebut adalah…
A. Persegi
B. Segitiga
C. Persegi Panjang
D. Lingkaran

Pembahasan Soal 2:
Mari kita analisis ciri-ciri yang diberikan:

• "Memiliki 4 titik sudut" dan "Keempat sudutnya adalah sudut siku-siku" – Ini bisa Persegi atau Persegi Panjang.
• "Memiliki 2 pasang sisi yang sama panjang" – Ini adalah ciri khas Persegi Panjang (panjang dan lebar berbeda). Jika semua sisi sama panjang, itu Persegi.

Jadi, jawaban yang tepat adalah C. Persegi Panjang.

Soal 3:
Benar atau Salah pernyataan di bawah ini:
a. Lingkaran tidak memiliki titik sudut. (__)
b. Sebuah segitiga selalu memiliki 4 sisi. (__)
c. Keliling persegi dihitung dengan menjumlahkan semua panjang sisinya. (__)
d. Luas persegi panjang dihitung dengan rumus panjang x lebar. (__)

Pembahasan Soal 3:
a. Benar. Lingkaran memang tidak memiliki titik sudut, hanya satu sisi lengkung.
b. Salah. Segitiga selalu memiliki 3 sisi, bukan 4.
c. Benar. Keliling bangun datar manapun, termasuk persegi, dihitung dengan menjumlahkan semua panjang sisinya. Rumus 4 x sisi adalah cara cepat untuk menjumlahkan 4 sisi yang sama panjang.
d. Benar. Rumus luas persegi panjang memang panjang x lebar.

Bagian 2: Menghitung Keliling Bangun Datar

Soal 4:
Sebuah taman berbentuk persegi memiliki panjang sisi 8 meter. Berapakah keliling taman tersebut?

Pembahasan Soal 4:

• Diketahui: Taman berbentuk persegi, panjang sisi (s) = 8 meter.
• Ditanya: Keliling taman.
• Rumus Keliling Persegi: Keliling = 4 x sisi
• Penyelesaian:
  Keliling = 4 x 8 meter
  Keliling = 32 meter

Jadi, keliling taman tersebut adalah 32 meter.

Soal 5:
Pak Budi ingin memagari kebunnya yang berbentuk persegi panjang. Panjang kebun adalah 15 meter dan lebarnya 9 meter. Berapa panjang pagar yang dibutuhkan Pak Budi?

Pembahasan Soal 5:

• Diketahui: Kebun berbentuk persegi panjang, panjang (p) = 15 meter, lebar (l) = 9 meter.
• Ditanya: Panjang pagar yang dibutuhkan (sama dengan keliling kebun).
• Rumus Keliling Persegi Panjang: Keliling = 2 x (panjang + lebar)
• Penyelesaian:
  Keliling = 2 x (15 meter + 9 meter)
  Keliling = 2 x (24 meter)
  Keliling = 48 meter

Jadi, panjang pagar yang dibutuhkan Pak Budi adalah 48 meter.

Soal 6:
Sebuah bingkai foto berbentuk segitiga memiliki panjang sisi-sisi 20 cm, 25 cm, dan 30 cm. Berapakah keliling bingkai foto tersebut?

Pembahasan Soal 6:

• Diketahui: Bingkai foto berbentuk segitiga, panjang sisi1 = 20 cm, sisi2 = 25 cm, sisi3 = 30 cm.
• Ditanya: Keliling bingkai foto.
• Rumus Keliling Segitiga: Keliling = sisi1 + sisi2 + sisi3
• Penyelesaian:
  Keliling = 20 cm + 25 cm + 30 cm
  Keliling = 75 cm

Jadi, keliling bingkai foto tersebut adalah 75 cm.

Soal 7:
Sebuah meja makan berbentuk lingkaran memiliki diameter 140 cm. Berapakah keliling meja makan tersebut? (Gunakan π = 22/7)

Pembahasan Soal 7:

• Diketahui: Meja makan berbentuk lingkaran, diameter (d) = 140 cm.
• Ditanya: Keliling meja makan.
• Rumus Keliling Lingkaran: Keliling = π x diameter (d)
• Penyelesaian:
  Keliling = (22/7) x 140 cm
  Keliling = 22 x (140/7) cm
  Keliling = 22 x 20 cm
  Keliling = 440 cm

Jadi, keliling meja makan tersebut adalah 440 cm.

Bagian 3: Menghitung Luas Bangun Datar

Soal 8:
Sebuah lapangan futsal mini berbentuk persegi dengan panjang sisi 10 meter. Berapakah luas lapangan futsal tersebut?

Pembahasan Soal 8:

• Diketahui: Lapangan berbentuk persegi, panjang sisi (s) = 10 meter.
• Ditanya: Luas lapangan.
• Rumus Luas Persegi: Luas = sisi x sisi
• Penyelesaian:
  Luas = 10 meter x 10 meter
  Luas = 100 m²

Jadi, luas lapangan futsal tersebut adalah 100 meter persegi.

Soal 9:
Sebuah lantai kamar berbentuk persegi panjang dengan panjang 6 meter dan lebar 4 meter. Jika lantai tersebut akan dipasangi keramik, berapakah luas area yang akan ditutupi keramik?

Pembahasan Soal 9:

• Diketahui: Lantai berbentuk persegi panjang, panjang (p) = 6 meter, lebar (l) = 4 meter.
• Ditanya: Luas area yang akan ditutupi keramik (sama dengan luas lantai).
• Rumus Luas Persegi Panjang: Luas = panjang x lebar
• Penyelesaian:
  Luas = 6 meter x 4 meter
  Luas = 24 m²

Jadi, luas area yang akan ditutupi keramik adalah 24 meter persegi.

Soal 10:
Sebuah hiasan dinding berbentuk segitiga memiliki alas 12 cm dan tinggi 8 cm. Berapakah luas hiasan dinding tersebut?

Pembahasan Soal 10:

• Diketahui: Hiasan dinding berbentuk segitiga, alas (a) = 12 cm, tinggi (t) = 8 cm.
• Ditanya: Luas hiasan dinding.
• Rumus Luas Segitiga: Luas = ½ x alas x tinggi
• Penyelesaian:
  Luas = ½ x 12 cm x 8 cm
  Luas = 6 cm x 8 cm
  Luas = 48 cm²

Jadi, luas hiasan dinding tersebut adalah 48 centimeter persegi.

Bagian 4: Soal Tantangan (Gabungan Konsep)

Soal 11:
Sebuah papan tulis berbentuk persegi panjang memiliki keliling 400 cm. Jika panjang papan tulis tersebut adalah 120 cm, berapakah luas papan tulis tersebut?

Pembahasan Soal 11:
Ini adalah soal dua langkah. Kita perlu mencari lebarnya terlebih dahulu menggunakan informasi keliling, baru kemudian menghitung luasnya.

• Diketahui: Papan tulis berbentuk persegi panjang, Keliling (K) = 400 cm, panjang (p) = 120 cm.
• Ditanya: Luas papan tulis.

Langkah 1: Mencari lebar (l) papan tulis.

• Rumus Keliling Persegi Panjang: K = 2 x (p + l)
• 400 cm = 2 x (120 cm + l)
• Bagi kedua sisi dengan 2:
  400 cm / 2 = 120 cm + l
  200 cm = 120 cm + l
• Kurangkan 120 cm dari kedua sisi:
  l = 200 cm – 120 cm
  l = 80 cm

Jadi, lebar papan tulis adalah 80 cm.

Langkah 2: Menghitung luas papan tulis.

• Rumus Luas Persegi Panjang: Luas = panjang x lebar
• Luas = 120 cm x 80 cm
• Luas = 9.600 cm²

Jadi, luas papan tulis tersebut adalah 9.600 centimeter persegi.

Soal 12:
Sebuah kebun bunga berbentuk persegi memiliki luas 81 m². Berapakah keliling kebun bunga tersebut?

Pembahasan Soal 12:
Ini juga soal dua langkah. Kita perlu mencari panjang sisi kebun terlebih dahulu dari luasnya, baru kemudian menghitung kelilingnya.

• Diketahui: Kebun bunga berbentuk persegi, Luas (L) = 81 m².
• Ditanya: Keliling kebun bunga.

Langkah 1: Mencari panjang sisi (s) kebun.

• Rumus Luas Persegi: L = sisi x sisi (atau s²)
• 81 m² = s x s
• Untuk mencari ‘s’, kita perlu mencari bilangan yang jika dikalikan dengan dirinya sendiri hasilnya 81. Bilangan tersebut adalah 9 (karena 9 x 9 = 81).
• s = 9 meter

Jadi, panjang sisi kebun adalah 9 meter.

Langkah 2: Menghitung keliling kebun bunga.

• Rumus Keliling Persegi: Keliling = 4 x sisi
• Keliling = 4 x 9 meter
• Keliling = 36 meter

Jadi, keliling kebun bunga tersebut adalah 36 meter.

Tips Belajar Bangun Datar untuk Siswa Kelas 4

Memahami bangun datar akan lebih mudah jika Anda menerapkan tips-tips berikut:

1. Pahami Konsep, Bukan Hanya Menghafal Rumus: Jangan hanya menghafal rumus, tapi pahami mengapa rumus tersebut digunakan. Misalnya, keliling adalah total panjang sisi, jadi wajar jika rumusnya adalah penjumlahan semua sisi.
2. Gambar Bangun Datarnya: Saat mengerjakan soal, biasakan untuk menggambar bangun datar yang dimaksud. Tuliskan ukuran yang diketahui pada gambar. Ini akan sangat membantu visualisasi masalah.
3. Perhatikan Satuan: Selalu periksa dan tuliskan satuan dengan benar (cm, m, cm², m²). Kesalahan satuan bisa mengubah arti jawaban.
4. Latihan Rutin: Semakin sering Anda berlatih, semakin terbiasa otak Anda dengan pola-pola soal dan penyelesaiannya.
5. Gunakan Benda di Sekitar: Lihatlah benda-benda di sekitar Anda (meja, buku, jam, jendela). Identifikasi bentuk bangun datarnya dan coba bayangkan bagaimana menghitung keliling atau luasnya. Ini membuat belajar lebih menyenangkan dan relevan.
6. Jangan Takut Bertanya: Jika ada yang tidak Anda pahami, jangan ragu bertanya kepada guru atau orang tua. Lebih baik bertanya daripada bingung sendiri.
7. Pecah Soal Menjadi Bagian Kecil: Untuk soal yang lebih kompleks (seperti soal tantangan), pecah masalah menjadi langkah-langkah kecil. Selesaikan satu per satu hingga mendapatkan jawaban akhir.

Penutup

Selamat! Anda telah menjelajahi berbagai konsep dan contoh soal bangun datar untuk kelas 4 SD. Ingatlah, matematika adalah tentang logika dan pemecahan masalah. Bangun datar adalah salah satu fondasi penting dalam matematika yang akan terus Anda gunakan di jenjang pendidikan selanjutnya.

Teruslah berlatih, jangan mudah menyerah, dan nikmati setiap proses belajar Anda. Dengan ketekunan dan pemahaman yang baik, Anda pasti akan menjadi ahli bangun datar! Semoga artikel ini bermanfaat dan menambah semangat Anda dalam belajar matematika.